Como Ingeniero de Software, hay etapas en el análisis de una solución donde es importante conocer algoritmos específicos, tales como los algoritmos de recorridos de nodos. Por consiguiente, el principal objetivo de este artículo es revisar los dos principales algoritmos de búsquedas en nodos conectados, los cuales son búsqueda en profundidad (en inglés DFS - ‘Depth First Search’) y búsqueda en anchura (en inglés BFS – ‘Breadth First Search’) para poder utilizarlos en favor de la eficiencia de un programa.
Búsqueda en Profundidad
Una búsqueda en profundidad (DFS) es un algoritmo de búsqueda para lo cual recorre los nodos de un grafo. Su funcionamiento consiste en ir expandiendo cada uno de los nodos que va localizando, de forma recurrente (desde el nodo padre hacia el nodo hijo). Cuando ya no quedan más nodos que visitar en dicho camino, regresa al nodo predecesor, de modo que repite el mismo proceso con cada uno de los vecinos del nodo. Cabe resaltar que si se encuentra el nodo antes de recorrer todos los nodos, concluye la búsqueda.
La búsqueda en profundidad se usa cuando queremos probar si una solución entre varias posibles cumple con ciertos requisitos; como sucede en el problema del camino que debe recorrer un caballo en un tablero de ajedrez para pasar por las 64 casillas del tablero.
En la figura a continuación se muestra un grafo no conectado, con ocho nodos, donde las flechas naranjas indican el recorrido del algoritmo DFS sobre los nodos.
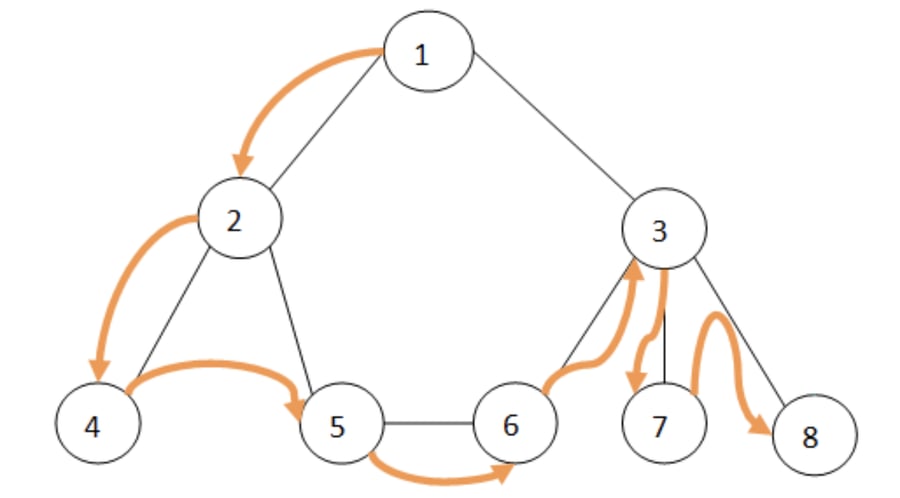
A continuación se muestra la implementación del algoritmo de búsqueda en profundidad en C++, donde se recorre los nodos del grafo usando un “iterador” que comienza desde el primer nodo hasta el último nodo ingresado. Se utiliza dos variables “nodoVisitado” y “nodoProcesado” para organizar el recorrido en profundidad, por esta razón se hace uso de la recursividad recorriendo los nodos en profundidad.
void DFS(grafo &g,int s){
nodoVisitado[s]=true;
procesarNodo(s);
list<int>::iterator it;
for(it=g.lados[s].begin(); it!=g.lados[s].end(); ++it){
if(!nodoVisitado[*it]){
nodoPadre[*it]=s;
DFS(g,*it);
}else if(!nodoProcesado[*it]){
procesarLado(s,*it);
}
}
nodoProcesado[s]=true;
}
Adicionalmente, se llamá a 2 funciones “procesarNodo” y “ProcesarLado” para observar el recorrido de los nodos como se muestra en la siguiente imagen:
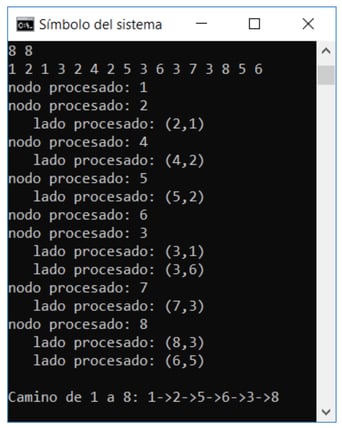
Nótese en la imagen de arriba que los 2 primeros dígitos (8, 8) representan el número de nodos y lados, seguidos por 8 pares de dígitos que representan las conexiones de los nodos. Finalmente se muestra el recorrido del algoritmo DFS desde el nodo 1 hacia el nodo 8.
Aplicaciones DFS
El algoritmo de búsqueda en profundidad tienes varias aplicaciones, entre las cuales tenemos las siguientes:
- Encontrar nodos conectados en un grafo
- Ordenamiento topológico en un grafo acíclico dirigido
- Encontrar puentes en un grafo de nodos
- Resolver puzzles con una sola solución, como los laberintos
- Encontrar nodos fuertemente conectados
En un grafo acíclico dirigido, es decir un conjunto de nodos donde cada nodo tiene una sola dirección que no es consigo mismo, se puede realizar un ordenamiento topológico mediante el algoritmo DFS. Por ejemplo, se puede aplicar para organizar actividades que tienen por lo menos alguna dependencia entre sí, a fin de organizar eficientemente la ejecución de una lista de actividades.
Los puentes en grafos son 2 nodos conectados de tal manera que para llegar a cada uno de sus extremos solo se puede a través de uno de esos nodos. Es decir, si removemos uno de los nodos ya no podremos acceder al otro nodo porque se han desconectado completamente. Esto se puede usar en la priorización de actividades que son representadas por nodos.
Si se quiere resolver un ‘puzzle’ o un laberinto, se puede resolver a través de DFS; los pasos de la solución pueden ser representados por nodos, donde cada nodo es dependiente del nodo predecesor. Es decir, cada paso de la solución del puzzle depende del anterior paso.
A veces será importante conocer qué tan conectados están ciertas actividades o componentes a fin de disminuir la dependencia de actividades o acoplamiento de componentes. Ésto con el objetivo de organizar en una mejor forma las actividades o agrupar de mejor modo los componentes porque así será más entendible el sistema; ésto también se puede resolver a través del algoritmo DFS.
Búsqueda en Anchura
Una búsqueda en anchura (BFS) es un algoritmo de búsqueda para lo cual recorre los nodos de un grafo, comenzando en la raíz (eligiendo algún nodo como elemento raíz en el caso de un grafo), para luego explorar todos los vecinos de este nodo. A continuación, para cada uno de los vecinos se exploran sus respectivos vecinos adyacentes, y así hasta que se recorra todo el grafo. Cabe resaltar que si se encuentra el nodo antes de recorrer todos los nodos, concluye la búsqueda.
La búsqueda por anchura se usa para aquellos algoritmos en donde resulta crítico elegir el mejor camino posible en cada momento del recorrido.
En la figura a continuación se muestra un grafo no conectado donde las flechas naranjas indican el recorrido del algoritmo BFS.
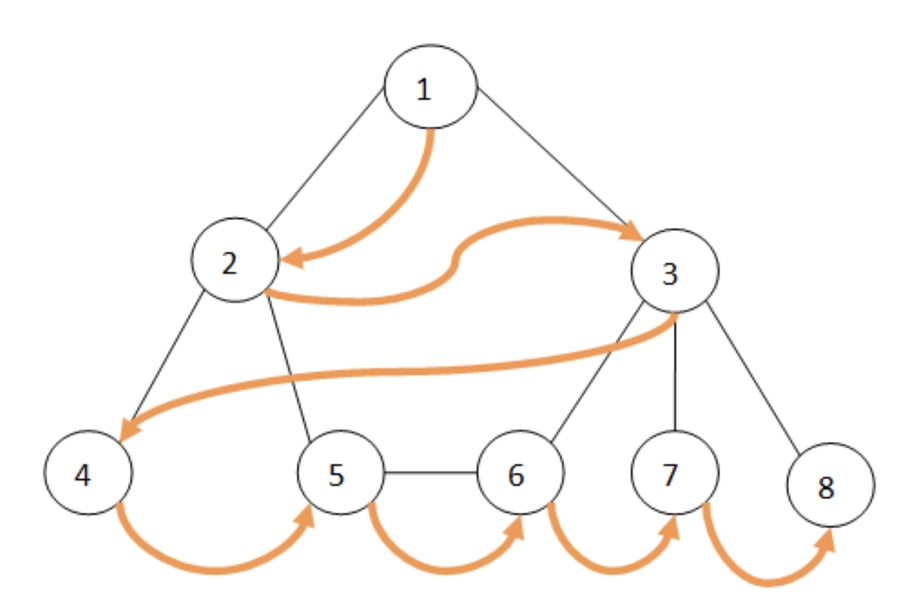
A continuación se muestra la implementación del algoritmo de búsqueda en anchura en C++, donde se recorren los nodos del grafo usando un “iterador” que comienza desde el primer nodo ingresado hasta el último nodo ingresado, recorriendo los nodos vecinos primeramente antes de los nodos hijos. Se utilizan dos variables “nodoVisitado” y “nodoProcesado” para organizar el recorrido en anchura. Por esta razón se hace uso de la estructura de datos cola (en inglés ‘queue’) para visitar los nodos en orden de llegada. Es decir, el primero procesa los nodos que primero llegaron a la cola.
void BFS(grafo &g,int s){
int v;
queue<int> cola;
list<int>::iterator it;
nodoVisitado[s]=true;
cola.push(s);
while(!cola.empty()){
v=cola.front(),cola.pop();
nodoProcesado[v]=true;
procesarNodo(v);
for(it=g.lados[v].begin(); it!=g.lados[v].end(); ++it){
if(!nodoVisitado[*it]){
cola.push(*it),nodoVisitado[*it]=true;
nodoPadre[*it]=v;
}
if(!nodoProcesado[*it]) {
procesarLado(v,*it);
}
}
}
}
Adicionalmente, se llama a 2 funciones “procesarNodo” y “ProcesarLado” para observar el recorrido de los nodos, como se muestra en la siguiente imagen:
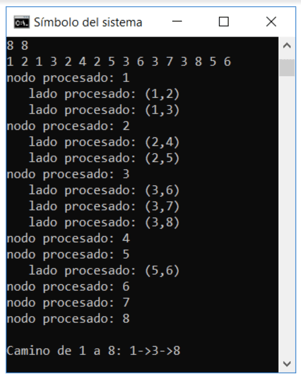
Nótese en la imagen de arriba que los 2 primeros dígitos (8, 8) representan el número de nodos y lados, seguidos por 8 pares de dígitos que representan las conexiones de los nodos. Finalmente, se muestra el recorrido del algoritmo BFS desde el nodo 1 hacia el nodo 8.
Aplicaciones BFS
El algoritmo de búsqueda en anchura tiene varias aplicaciones, entre las cuales tenemos las siguientes:
- Encontrar el camino más corto entre 2 nodos, medido por el número de nodos conectados
- Probar si un grafo de nodos es bipartito (si se puede dividir en 2 conjuntos)
- Encontrar el árbol de expansión mínima en un grafo no ponderado
- Hacer un Web Crawler
- Sistemas de navegación GPS, para encontrar localizaciones vecinas
En grafos no ponderados (los nodos no tienen una medida o peso), mediante el algoritmo BFS es posible encontrar el camino más corto. Por ejemplo, si tenemos un conjunto de actividades representadas por nodos y deseamos llegar a una actividad específica realizando la menor cantidad de actividades posibles, podemos usar este algoritmo; en el caso que tengamos un grafo ponderado para el ejemplo anterior donde las actividades tengan un tiempo estimado, podemos modificar el algoritmo BFS, llegando a obtener el algoritmo Dijkstra.
En teoría de códigos, para decodificar palabras-código, es posible usar BFS para probar si el grafo de nodos es bipartito con el objetivo de verificar que la información no esté corrompida. Por ejemplo, en el grafo de Tanner, en donde los nodos de un lado de la bipartición se representan por dígitos de una palabra-código y los nodos del otro lado representan las combinaciones de los dígitos que se espera que sumen cero en una palabra-código sin errores.
Encontrar el árbol de expansión mínima en un grafo no ponderado es otra aplicación del algoritmo BFS. Por ejemplo si se desea recorrer un conjunto de lugares sin pasar dos veces por el mismo lugar, se puede usar este algoritmo.
Si queremos realizar un buscador de sitios web como Google, podemos acceder al DOM (Document Object Model) mediante un Web Crawler, un algoritmo que suele usar búsquedas en anchura para recorrer las etiquetas HTML, de modo que podemos limitar los niveles de búsquedas en el DOM.
En sistemas de Navegación GPS, podemos usar BFS para encontrar lugares cercanos de interés. Por ejemplo, si tenemos un conjunto de lugares turísticos y servicios representados por nodos conectados entre sí en base a su proximidad geográfica, entonces podemos obtener un listado de lugares turísticos cercanos, lo cual puede ser utilizado para planear un viaje o una excursión.
Conclusión
A través de los algoritmos mencionados en este artículo, se puede encontrar caminos o recorridos entre dos o más nodos dependiendo de la naturaleza del problema. Por ejemplo, se puede usar el algoritmo BFS en mapas de Google para encontrar rutas óptimas entre puntos turísticos de interés o para hacer búsquedas de textos en una página web por medio de un Web Crawler; por medio del algoritmo DFS, se puede resolver o simular juegos como laberintos o ajedrez.
